60 lines
1.4 KiB
Markdown
60 lines
1.4 KiB
Markdown
# 矩阵
|
||
|
||
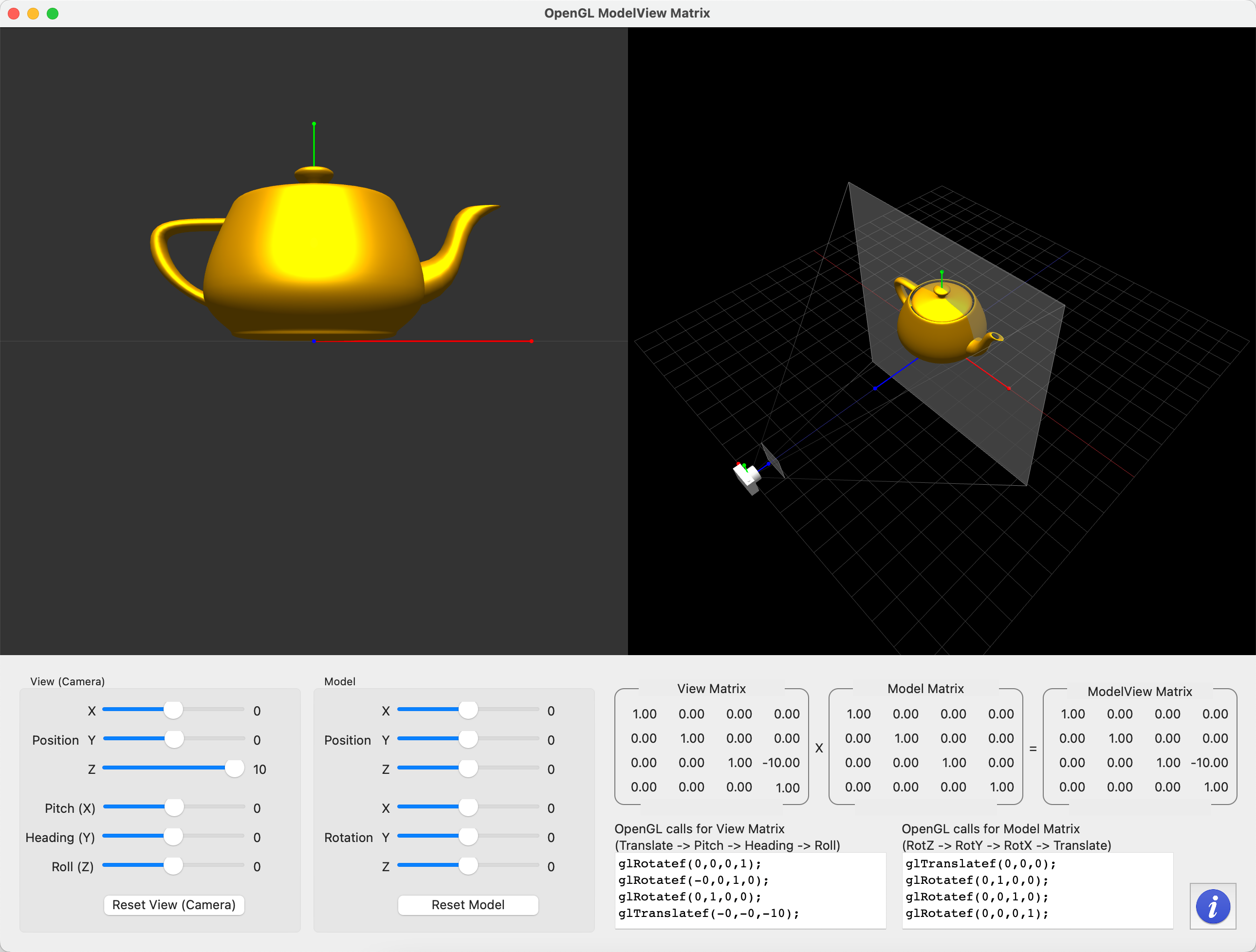
在3D计算机图形学中,4x4矩阵最常用的用法是作为一个变换矩阵Transformation Matrix。
|
||
|
||
|
||
|
||
Matrix4
|
||
|
||
矩阵可以直接看成二维数组。
|
||
|
||
|
||
|
||
什么是三维投影转换? 简而言之,就是将三维空间中的物体,投射在相机视平面的转换算法
|
||
|
||
三维投影矩阵计算公式如下:
|
||
|
||
```shell
|
||
const uMatrix = ProjectMatrix * CameraMatrixWorldInverse* ObjectMatrixWorld
|
||
```
|
||
|
||
视图矩阵称为**ViewMatrix**
|
||
|
||
视图矩阵的含义是,固定其他因素,我们改变了相机的位置和角度后,它眼中的世界也会发生变化,这种变化就是视图矩阵。
|
||
|
||
|
||
### 获取屏幕二维坐标
|
||
|
||
给定三维坐标[x, y, z],怎么获取它在屏幕上的二维坐标呢?计算公式如下:
|
||
|
||
```shell
|
||
const [x, y] = ProjectionMatrix * CameraWorldMatrixInverse * [x, y, z]
|
||
```
|
||
|
||
THREE在Vector3上封装了方法:
|
||
|
||
```shell
|
||
const v = new THREE.Vector3(x, y, z);
|
||
const xy = v.project(camera);
|
||
```
|
||
|
||
### 屏幕坐标转化为三维坐标
|
||
|
||
|
||
给定屏幕二维坐标[x, y],怎么获取它在三维空间中三维坐标呢?计算公式如下:
|
||
|
||
```shell
|
||
const [x, y, z] = CameraWorldMatrix * ProjectionMatrixInverse * [x, y, z]
|
||
```
|
||
|
||
```shell
|
||
const v = new THREE.Vector3(x, y, z);
|
||
const xyz = v.unproject(camera);
|
||
```
|
||
|
||
|
||
|
||
|
||
## 文档
|
||
|
||
https://threejs.org/docs/#api/zh/math/Matrix4 |